Minimum fluid velocity required to keep a check valve fully open.

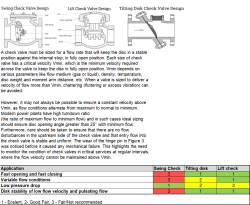
A check valve must be sized for a flow rate that will keep the disc in a stable position against the internal stop, in fully open position. Each size of check valve has a critical velocity V(min), which is the minimum velocity required across the valve to keep the disc in fully open position.

This calculation addresses a fundamental principle in fluid mechanics related to check valves: each check valve requires a minimum fluid velocity to remain fully open and stable.

The core principle involves the balance of forces. For a check valve to remain fully open:

• The fluid's dynamic pressure force must overcome the disc's weight and any spring forces
• This prevents "chattering" or unstable oscillation of the valve disc
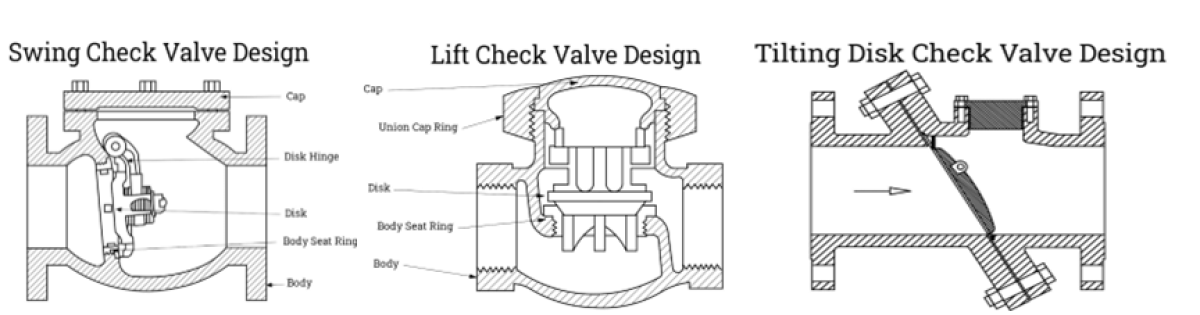
• Different valve designs (swing, lift, tilting disc) have different minimum velocity requirements based on their geometry and mounting orientation

The calculation determines this critical minimum velocity (Vmin) using empirical coefficients that account for:

• Valve type and configuration (represented by coefficient C in the equations)
• Fluid density (q in the calculation)
• Flow area ratio between valve port and pipe (β)

Once this minimum velocity is determined, it can be converted to a flow rate requirement by multiplying by the flow area.

Understanding this principle is important because:

• Operating below this minimum velocity causes valve instability and accelerated wear
• Proper valve selection must account for the full range of expected flow conditions
• The calculation helps engineers avoid premature valve failure and system inefficiencies

This represents a classic application of fluid dynamics principles to practical mechanical component design.